Bethany
Marko
Help Your Child Succeed in English
Lucy
Teerth
Stefan
hadi
Phua Sui
Hibah
Anna
Sharyn
Noma
Swati
JIthendra Varma
Elizabeth
Angelpreet
Anagha
Prachi
Shaunak
Hassan
Feba
Buddhima
Priyank
Sukhvir
Local Reviews
From the first session Georgia just adores her! In just 2 sessions we’ve already seen a huge change In her attitude, she looks forward to tutoring now! Emily jo is simply amazing!!!!Nicole, Gulfview Heights
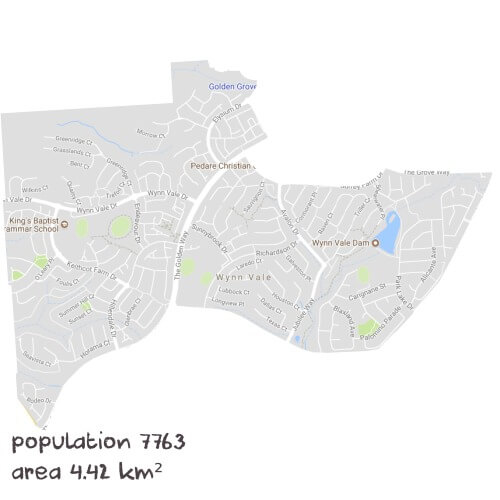
Inside Wynn ValeTutoring Sessions
Content Covered
Year 4 student Jasmine worked on arranging fractions and decimals on a number line and explored how to convert between the two.
In Year 10, Sam focused on the area of a triangle formula with practical applications, then built confidence in function notation and reviewed key physics formulas ahead of an upcoming test.
For Year 11, Mia practiced using the sine and cosine rules for non-right-angled triangles, revisited area of a triangle calculations, and discussed strategies for applying these in complex questions.
Recent Challenges
A Year 10 student hesitated to ask questions during Biology, even when unsure about homeostasis concepts; as one tutor noted, "she still second guesses herself occasionally." This reluctance meant she missed out on valuable clarification before a mock test.
In Year 11 Maths, time management issues led to incomplete homework and last-minute revision, leaving some modules unfinished before deadlines.
Meanwhile, a Year 7 student's written working in algebra was difficult to follow due to inconsistent layout—extra time was spent deciphering steps rather than tackling new material.
Each instance highlights how process habits shaped both understanding and progress in class.
Recent Achievements
A tutor in Wynn Vale noticed a Year 11 student who used to avoid asking questions now regularly checks her understanding out loud and even requested extra practice before her physics test—her recent grade reflected that extra effort.
Another high school student, initially hesitant to trust her own answers, has started double-checking her work independently and completing more homework without prompting.
In the younger years, one previously shy primary student now volunteers to read short passages aloud during spelling sessions, something she never attempted at the start of tutoring.