Exponential functions are functions with constant bases and variables in their exponents, which find a lot of use in real life. In this article, we will not only learn how to graph basic exponential functions, but we will also learn how to find the slopes of simple and more complex exponential functions.
Learning Outcomes
By the time you finish reading this page, you will have learned about
- Exponential functions and their graphs
- Euler’s number and its significance
- Natural logarithms
- Differentiating exponential functions using the chain rule
What’s an Exponential Function?
Think about the function \(y=2^x\). What should it look like? Grab a sheet of paper and draw a rough sketch. If you get stuck, you can plug in simple numbers such as x = -2, -1, 0, 1 and 2 into the equation. The outputs are \(\frac{1}{4},\frac{1}{2},\), 1, 2, and 4, respectively.
Let’s plot them on the coordinate plane as shown below.
As you can see, the graph rises exponentially (unlike a linear function that gives a straight line).
Any clue as to what happens if we change the 2 in the equation (called the base) to a 3? Or make it less than 1, like \(\frac{1}{2}\)?
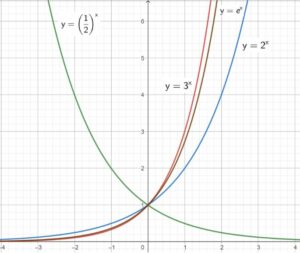
Resist the temptation to graph them on a calculator. Instead, pick some easy values of x as you did before, find the corresponding y values, and plot them. The graphs are shown in the figure below. We’ve plotted all three on the same coordinate plane so that it’s easy to compare them. We also included the graph of \(y=e^{x}\), where e is Euler’s Number. It is an extremely important graph that you will encounter many more times during your Year 11 (and 12) HSC Advanced Math course.
Quick question: why do you think the graph of \(e^{x}\) is between the graphs of \(2^{x}\) and \(3^{x}\)?
Take a moment to reflect on your learnings:
- If the base is larger than 1 (like 2 and 3), the graph increases exponentially from left to right. This is called exponential growth
- If the base is smaller than 1 (like ½), the graph decreases exponentially from left to right. This is called exponential decay
- The x-axis is an asymptote. An asymptote is a straight line a graph approaches but never touches. Quick question: why do you think these graphs never touch or cross the x-axis?
- The y-intercepts are all equal to 1 (again, why?).
- The graphs of \(2^{x}\) and \((\frac{1}{2})^{x}\) are symmetrical (mirror reflections) about the y-axis.
Exponential Functions in Real Life
Exponential functions are everywhere around us! Here are just a few examples of where you might see exponential functions in action:
1. Population growth: The world population is growing at an exponential rate. Every day, there are more and more people on the planet.
2. Virus spread: When a virus starts to spread, it usually does so exponentially. This is why viruses like COVID-19 can be so difficult to control!
3. Interest: An exponential model is used to calculate the interest you earn in your savings account.
4. Carbon dating: This technique for dating archaeological samples uses the fact that radioactive isotopes decay exponentially.
A (brief) introduction to Euler’s Number
There’s an irrational number, called ‘e’, named after a Swiss Mathematician named Leonhard Euler, that finds a lot of use in real life. Its value is 2.718….
Although you don’t have to, it’s expected that as a high school Science student, you will memorize this number at least up to 3 digits after the decimal point.
The beauty is, ‘e’ not only limits itself to your Maths and Physics books, but it also shows up in some patterns in the real world! If you are curious to know more about this wonderful irrational number, watch this video.
Need help preparing for your Year 11 Exponential Functions? Contact us now!
Natural Logarithm
You have learned about logarithms in your previous years. Until now, the base of every logarithmic expression you came across was 10. In Calculus, you will deal a lot with logarithms with base e. A logarithm with base e is called a natural logarithm. It is denoted by ln.
When we write lnx, we mean \(log_{e}x\). Note that lne = 1.
Derivative of Exponential Functions
The derivative of an exponential function \(f(x)=a^x\) is given as \(f'(x)=a^xlna\). This means that the derivative of \(y=e^x\) is \(e^x\) (as lne = 1).
Take a moment to reflect this: there’s an exponential function with varying slopes at different values of x, and the slope at each point is exactly the same as the value of the function (y) at that point! How’s that even possible? Well, this is one of the many reasons why this number is so special!
You can use the chain rule to find the derivative of more complex exponential functions.
\(\frac{d(e^u)}{dx}=\frac{d(e^u)}{du}\times \frac{du}{dx}=e^u\frac{du}{dx}\)
Example:
If \(f(x)=e^{2x+3},\) find \(f'(x).\)
Solution:
Applying the chain rule we have \(f'(x)=e^{2x+3}\times \frac{d(2x+3)}{dx}=e^{2x+3}\times 2=2e^{2x+3}\)
Wrap Up
Exponential functions have countless applications in Science and real life. We hope this article helped you understand exponential functions and their graphs. Differentiating exponential functions using the chain rule can be tricky, but we can promise that practice will make it easy. If you’re still struggling, don’t hesitate to seek help.