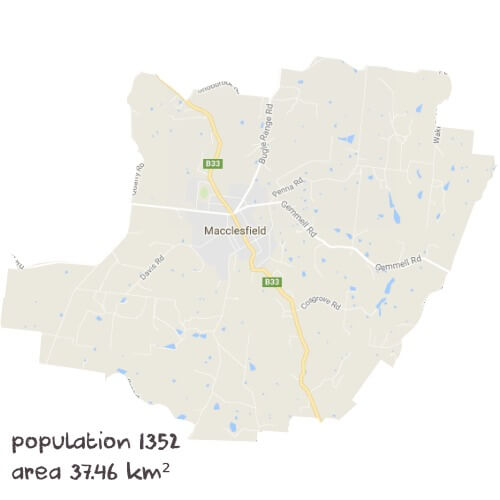
Mitchell
Local Reviews
We loved Richard, he was kind, patient and a great teacher. My son really enjoyed working with him and we loved having Richard in the house. He was always on time, respectful and organised.Sue
Inside MacclesfieldTutoring Sessions
Content Covered
Year 4 student Sophie practised multiplication with large numbers and explored equivalent fractions, using number games to reinforce understanding.
Year 5 Annabelle worked through probability worksheets from school and created graphs from tables, focusing on interpreting data visually.
For Year 4 Sydney, lessons focused on building multiplication and division skills with textbook exercises, as well as introducing fraction equivalence and representing fractions on a number line.
Recent Challenges
A Year 7 student repeatedly rushed through maths questions, often missing key details and making unnecessary calculation errors—"she keeps trying to rush the answers and is therefore making silly mistakes."
This habit meant she frequently second-guessed her work and needed reassurance at every step, especially when placing numbers on a number line or interpreting worded problems.
In Year 10, another student struggled with multi-step fraction tasks; instead of reviewing unfamiliar material, she gravitated towards easier revision and hesitated to attempt more complex connections between fractions and division.
Tiredness sometimes led both students to leave homework incomplete or avoid challenging tasks altogether.
Recent Achievements
A tutor in Macclesfield noticed that Jay, a high school student, now regularly spots and corrects his own mistakes during division problems—something he hesitated to do before.
Annabelle, also in high school, has started approaching problem-solving questions without waiting for prompts and was quick to explain her reasoning for dividing percentages by 100 before multiplying—a step she'd often missed in the past.
Meanwhile, Sydney from Year 6 surprised herself by moving on from basic multiplication to tackling advanced problems like 14 x 52 independently after gaining confidence with earlier questions.