Yahui
Yaseen
Help Your Child Succeed in Maths
Jeshta
Yu On
Majid Mehmood
Dominic
Thomas
Yuan
IFTEKAR
Trieu Anh
Jiale
Danielle
Ankur
Miles
Shilpa
Melanie
Sachintha
Marie Gindria
Matthew
Emma
Rajyavardhan
Carol
Sharat
Local Reviews
The whole process was really easy. We switched sessions a few times and nothing was a problem for them, they were very accommodating.Anne, Putney
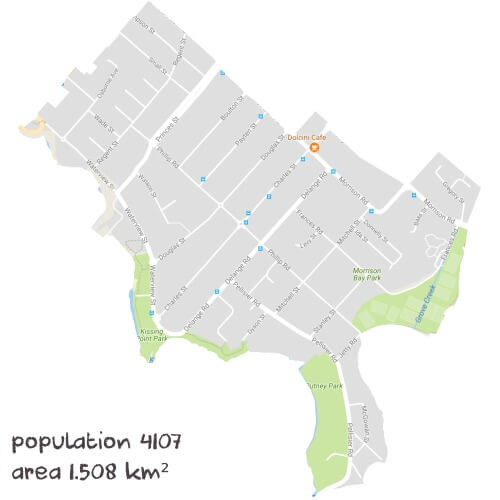
Inside PutneyTutoring Sessions
Content Covered
Year 8 student Amber worked through a chemistry worksheet on radioactive decay and also reviewed chemical bonding for an upcoming assessment.
In Year 10, Michael focused on interpreting box and whisker plots to understand range and interquartile range, alongside tackling data processing questions from his textbook.
Meanwhile, Year 6 student Liam practiced the basics of trigonometry using right-angled triangle problems, reinforcing foundational skills with targeted exercises.
Recent Challenges
A Year 10 student struggled to recall past mathematics content quickly, with a tutor noting, "she needs to practice more and do the homework," as life distractions affected her focus.
In Year 12 Economics, one student was advised to review case study work before an exam but showed a tendency to only revise familiar material rather than tackle new essay structures or definitions.
For a Year 8 student, difficulty arose in remembering which formulae applied during circle problems, especially without regular revision.
When confidence dropped after setbacks—like confusing equation labels in Year 9—the urge to avoid challenging tasks crept in.
Recent Achievements
A tutor in Putney noticed one Year 12 student who had struggled with writing structured business report paragraphs was able to produce her first full paragraph independently last session—a real leap from needing step-by-step guidance.
In a recent Year 11 economics session, a student who previously missed links between inflation and other objectives could now explain these connections without prompting, showing clear growth in analytical thinking.
Meanwhile, Erin in Year 6, who often hesitated with new problem-solving methods, began using a "work backwards" approach for network questions after some encouragement and stuck with it through the whole worksheet.