Aagam
Faraz
Help Your Child Succeed in Chemistry
Talal
Aarya
Pragya
rahath
monish
Rubaina
Awais
Fadil
Matthew
William
Edward
Ismath Maryam
Haozheng (Steven)
Mariam
Jordan
Shashini
Justin
Roy
Anthony
Bikram
Local Reviews
Tutoring with Tiger has been a great start for Mahi. Tiger is a dedicated tutor.Bhavini
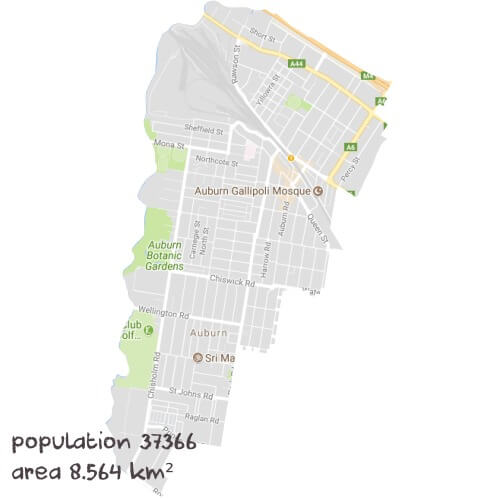
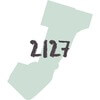
Inside AuburnTutoring Sessions
Content Covered
Year 8 student Alex worked through algebraic expansion and simplification, including a brief introduction to factorisation.
For Year 9, Sarah focused on solving equations involving negative numbers and converting between improper fractions and mixed numbers, using worked examples for clarity.
Meanwhile, Year 5 student Ethan practised multiplication tables and tackled both short and long division problems to strengthen calculation speed and accuracy.
Recent Challenges
In Year 8 Maths, one student repeatedly arrived late and struggled to remember parallel line rules even after several lessons; as noted, "late for 15 mins… confused about parallel lines rules after 3 lessons." This time lost meant homework was often completed during the session itself.
In a senior class (Year 12), another student did not complete assigned homework due to weekend commitments like camp and soccer, leading to in-session catch-up rather than new learning.
Meanwhile, a Year 10 student's over-reliance on mental calculations in algebra led to missed sign errors—"he skipped showing steps in algebra, which hid sign errors"—forcing them to retrace their logic under test conditions.
Recent Achievements
A tutor in Auburn recently noticed Georgia, a high school student, clearly explaining significant figures back to the tutor after initially struggling with the topic—she even used a flipped learning approach to reinforce her understanding.
Another high school student began openly asking questions whenever confused instead of staying quiet; this shift meant he quickly fixed errors during exam review and completed 25% of his paper more accurately than before.
Meanwhile, Noah in Year 4 has started solving two-digit addition problems much faster and now consistently remembers to carry forward—a step he used to miss.