Florian
Kenza
Help Your Child Succeed in Maths
Joseline
Lilly
Ethan
Ben Peishen
Holly
John
Yu sum
Rodrigo
Vedant
Alita
Rodrigo
Milan Chirayath
Mamta
Dziila
Hui Han Hannie
Anil
So Yeon
Jenna
Nikola
Emily
Sacha
Local Reviews
We are very happy with Thilac. He is very good with Zac and knows his stuff.Kathryn, Teneriffe
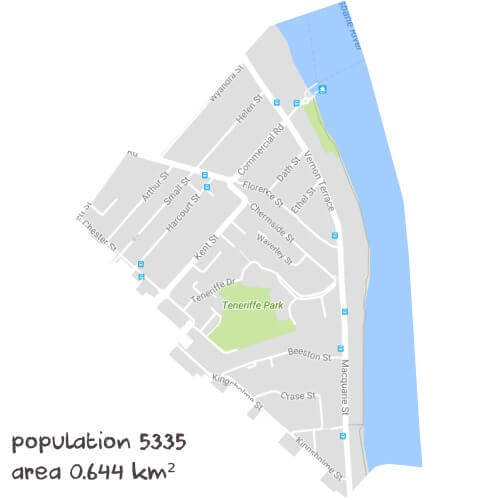
Inside TeneriffeTutoring Sessions
Content Covered
Year 7 student Emily worked through adding, multiplying, and dividing fractions as well as converting between decimals and fractions for fluency.
In Year 10, Zoe focused on solving compound interest problems and practiced using the power law to simplify indices.
Meanwhile, Year 11 student Jack revised calculus skills including finding derivatives of exponential functions with the chain rule and applied these methods to solve optimisation questions involving maximum and minimum values.
Recent Challenges
Homework completion was a recurring issue for both Year 8 and Year 11 students, with "amount of homework done due to assignments is still lacking," leading to gaps in practice—especially in algebra and statistics.
In a Year 10 English assignment, referencing errors and overloaded body paragraphs signaled difficulty organizing ideas under time pressure.
A Year 12 student working on calculus repeatedly hesitated to start complex problems: "did not know where to start… need to push for more engagement."
One tutor noted a Year 9 student's tendency to avoid writing out steps in logarithms, which meant calculation slips were hard to trace later.
Recent Achievements
A tutor in Teneriffe noticed a Year 11 student who previously hesitated to show her reasoning for problem-solving questions is now confidently writing out her approach, moving beyond just thinking through the steps silently.
In another high school session, a student who struggled with identifying errors during revision began recognising when to apply the chain rule while working through sin and cos calculations—something that had tripped them up before.
Meanwhile, a Year 4 student who often made mistakes with fractions started independently applying addition and multiplication of fractions correctly during their last session.