Rabeeta
Madhur
Help Your Child Succeed in Physics
Anu Priya
Anureet
Jeremy
Mahak
Rohit
Vinil
Pooja
Vandana
Rupandeep
Samuel
Soma
Piraveen
Faiqa
afra
Srijan
Akhilan
Alvin
Rajalakshmi
Jessica
Rutvik
Monika
Local Reviews
Jayesh was excellent.Antonino
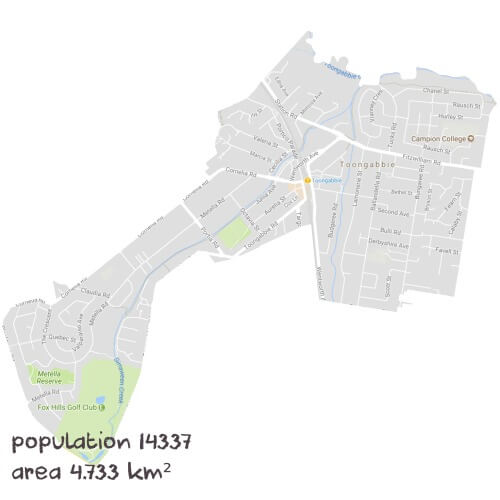
Inside ToongabbieTutoring Sessions
Content Covered
Year 8 student Aman focused on solving simultaneous equations using both elimination and substitution methods, and also practised graphing linear equations from given formulas.
Year 11 student Grace revised differentiation techniques for trigonometric functions as part of the Stage 6 Maths Advanced calculus curriculum, then moved to integration problems involving exponentials and logarithms.
Meanwhile, Year 12 student Priya tackled Financial Mathematics by calculating compound interest and worked through sequences in arithmetic series, reinforcing these with targeted exam-style questions.
Recent Challenges
In Year 8 algebra, one student's tendency to copy notes too quickly led to missing signs—"he would be copying notes but miss a sign or two because he go past too fast"—resulting in confusion when factorising expressions.
For a Year 11 trigonometry graphing task, another struggled with interpreting questions that were "a little wordy," making it harder to tackle exam-style problems without pausing to fully read instructions.
In both cases, the urge to rush or avoid careful reading meant extra time was spent fixing errors rather than building fluency with more challenging material.
Recent Achievements
During a Toongabbie tutoring session, Grace, a high school student, tackled her recent exam with noticeably greater independence. She earned most of her marks in financial mathematics and statistics after previously hesitating on multi-step problems.
Another tutor noted Oliver, also in high school, who now solves financial calculation questions quickly and confidently, having struggled before to select the right formulas without prompting.
Meanwhile, Isaac in Year 6 has started asking clarifying questions about his assignments rather than waiting for hints. This shows a real shift from passive participation to active engagement during lessons.